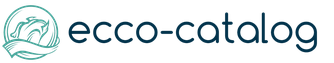координати на целта, радарни мерки; ъгъла на атака на самолета; натоварване в електрическата верига.

5. Видове случайни процеси.

В математиката съществува концепцията за произволна функция.

Случайна функция- функция, която в резултат на опита придобива една или друга специфична форма, и която не е известна предварително. Аргументът за такава функция не е случаен. Ако аргументът е време, тогава се извиква такава функция произволен процес... Примери за произволни процеси:

Особеността на произволна функция (процес) е, че при фиксирана стойност на аргумента (t), произволната функция е произволна променлива, т.е. при t = t i X (t) = X (t i) е произволна променлива.

Ориз. 2.1. Графично представяне на произволна функция

Стойностите на произволна функция за фиксиран аргумент се наричат ​​нейна секция. Защото произволна функция може да има безкраен набор от секции и във всеки раздел е произволна променлива, тогава произволната функция може да се разглежда като безкраен случаен вектор.

Теорията на случайните функции често се нарича теория на случайността (стохастична)

процеси.

За всяка секция от произволен процес можете да посочите m x (t i), D x (t i), x (t i) и в общия случай - x (t i).

В допълнение към случайните функции на времето, понякога се използват случайни функции на координатите на точка в пространството. Тези функции привеждат в съответствие с всяка точка в пространството някаква случайна променлива.

Теорията на случайните функции на координатите на точка в пространството се нарича теория на случайното поле... Пример: векторът на скоростта на вятъра в турбулентна атмосфера.

В зависимост от вида на функцията и типа на аргумента има 4 типа произволни процеси.

Таблица 2.1 Видове случайни процеси

размер на локва (непрекъсната стойност)

Освен това се прави разлика между:

1. Стационарен произволен процес- чиито вероятностни характеристики не зависят от времето, т.е. x (x 1, t 1) = x (x 2, t 2) =… x (x n, t n) = const.

2. Нормален произволен процес (Гаусов)- съвместна вероятностна плътност на напречните сечения t 1… t n - нормално.

3. Марков случаен процес(процес без последствия) състоянието, във всеки момент от време, което зависи само от състоянието в предходния момент и не зависи от предишните състояния. Марковската цел е последователност от секции на произволен процес на Марков.

4. Случаен тип процесбял шум - във всеки момент от състоянието не зависи от предишния.

Има и други случайни процеси.

Извиква се функция, чиято стойност за всяка стойност на независимата променлива е произволна променлива произволна функция. Извикват се произволни функции, за които независимата променлива е времето произволни процеси или стохастични процеси .

Случайният процес не е определена крива, това е набор от определени криви, където, получена в резултат на индивидуални експерименти (фиг. 1.9). Всяка крива от това множество се нарича изпълнението на произволен процес . Невъзможно е да се каже предварително кое изпълнение ще последва процесът.

За всеки фиксиран момент от времето, например, изпълнението на случаен процес е специфична величина, докато стойността на произволна функция е произволна променлива, наречена напречно сечение произволен процес в даден момент . Следователно не може да се твърди, че произволен процес в даден момент от време има такава и такава детерминирана стойност; можем да говорим само за вероятността в даден момент от време стойността на произволен процес като случайна променлива да бъде в определени граници.

Ориз. 1.9. Изпълнения на произволни процеси

Статистическите методи изучават не всяка една от реализациите, които образуват множество, а свойствата на цялото множество като цяло, като осредняват свойствата на включени в него реализации. Следователно при изследване на контролен обект поведението му се оценява не по отношение на някакво конкретно въздействие, което представлява дадена функция на времето, а по отношение на цял набор от влияния.

Както е известно, статистическите свойства на произволна променлива се определя от неговата функция на разпределение на вероятностите на интеграла и диференциал .

За произволен процес също се въвежда концепцията за функция на разпределение и плътност на вероятността, които зависят от фиксирано време на наблюдение и от определено избрано ниво, тези. са функции на две променливи и.

Помислете за произволна променлива , т.е. част от произволен процес в момент от време. Едновариантна функция на разпределение произволен процес е вероятността текущата стойност на произволен процес в даден момент да не надвишава определено определено ниво (число) , т.е.

Ако функцията има частична производна по отношение на, т.е.

тогава функцията се извиква едномерна плътност на вероятността произволен процес. Величината

представлява вероятността да е в интервала от преди.

Във всеки един момент от времето наблюдаеми случайни променливи (секции от случаен процес) ще имат свои собствени, като цяло различни, едномерни функции на разпределение и плътности на вероятностите.

Функции и са най-простите статистически характеристики на случаен процес. Те характеризират произволен процес изолирано в отделните му участъци, без да разкриват взаимната връзка между участъците на произволния процес, т.е. между възможните стойности на произволния процес в различни моменти от време.

Познаването на тези функции все още е недостатъчно, за да се опише случаен процес в общия случай. Необходимо е също така да се характеризира взаимосвързаността на произволни променливи в различни произволни моменти.

Нека сега разгледаме случайни променливи и, като се позоваваме на две различни точки от времето и наблюдение на случаен процес.

Вероятността произволен процес ще бъде не повече от в , тези.

са наречени функция на двумерно разпределение ... Ако функцията има частични производни poi, т.е.

, (1.47)

тогава функцията се извиква двумерна плътност на вероятността .

Величината

е равна на вероятността тя да пристигне в интервала от до и за в диапазона от до.

По същия начин може да се въведе понятието за n-мерна функция на разпределение и n-мерна плътност на вероятността .

Колкото по-висок е порядъкът, толкова по-пълно са описани статистическите свойства на произволен процес. Познавайки -мерната функция на разпределение, от нея е възможно да се намерят едномерни, двумерни и други [до -ти] функции на разпределение от по-нисък порядък. Въпреки това, многоизмерните закони за разпределение на случайните процеси са относително тромави характеристики и е изключително трудно да се работи с тях на практика. Следователно при изследването на стохастичните процеси те често се ограничават до случаите, когато за описание на стохастичен процес е достатъчно да се знае само неговият едномерен или двумерен закон на разпределение.

Пример за произволен процес, който се характеризира напълно с едномерна плътност на вероятностите,е т.нар чист произволен процес, или бял шум . Стойностите в този процес, взети в различни моменти от време, са напълно независими една от друга, без значение колко близки са тези моменти във времето. Това означава, че кривата на белия шум съдържа изблици, които се разпадат в безкрайно малки интервали от време. Тъй като стойностите, например, в моменти от време са независими, вероятността за съвпадение на събития, състояща се в намиране между и в момента и между и в момента, е равна на произведението на вероятностите на всяко от тези събития, следователно

и общо взето за бял шум

т.е., всички плътности на вероятностите за бял шум се определят от едномерната плътност на вероятността.

За произволни процеси с обща форма, ако е известно какви стойности е взела стойността в момента, по този начин имаме известна информация за това къде, тъй като стойностите и, най-общо казано, са зависими. Ако освен да се знае къде, тогава информацията се увеличава още повече. Така увеличаването на познанията ни за поведението на процеса до момента води до факта, че информацията за.

Съществува обаче специален клас случайни процеси, изследван за първи път от известния математик А. А. Марков и наречен Марков случайни процеси , за което знанието за стойността на процеса в момента вече съдържа цялата информация за бъдещия ход на процеса, която може да бъде извлечена само от поведението на процеса до този момент. В случай на стохастичен процес на Марков, за да се определят вероятностните характеристики на процеса в даден момент от време, е достатъчно да се знаят вероятностните характеристики за всеки един предходен момент от време, например непосредствено предхождащ момент от време. Познаването на вероятностните характеристики на процеса за други предишни стойности на времето, например, не добавя информация, необходима за намиране.

За процес на Марков е валидно следното отношение:

, (1.51)

т.е. всички плътности на вероятностите на процеса на Марков се определят от двумерната плътност на вероятностите. С други думи, произволните процеси на Марков се характеризират напълно с двумерна плътност на вероятностите.

Концепцията за функцията на разпределение и плътността на вероятността на случаен процес обикновено се използва в теоретичните конструкции и дефиниции. В практиката на изследванията широко разпространени са относително по-прости, макар и по-малко пълни характеристики на случайни процеси, аналогични на числените характеристики на случайните величини. Примери за такива характеристики са математическото очакване, дисперсията, средната стойност на квадрата на произволен процес, корелационна функция, спектрална плътност и други.

Математическо очакване (средна стойност) на произволен процес е стойността

(1.52)

където - едномерна плътност на вероятността на случаен процес .

Математическото очакване на случаен процес е някаква неслучайна (редовна) функция на времето, около който се групират всички реализации на даден случаен процес и спрямо който се колебаят (фиг. 1.10).

Математическото очакване на произволен процес във всеки фиксиран момент от време е равно на математическото очакване на съответния участък от произволния процес. Математическото очакване се нарича средната стойност на произволен процес върху множеството (средната по ансамбъла, средната статистическа), тъй като това е вероятностно осреднената стойност на безкраен набор от реализации на случаен процес.

Ориз. 1.10. Числени характеристики на случайни процеси

Често се въвежда под внимание центриран произволен процес

Тогава произволен процес може да се разглежда като сбор от два компонента: редовен компонент, равен на математическото очакване, и центриран случаен компонент, т.е.

За да се вземе предвид степента на дисперсия на изпълнението на произволен процес спрямо неговата средна стойност, се въвежда понятието дисперсия произволен процес, който е равен на математическото очакване на квадрата на центрирания случаен процес:

. (1.55)

Дисперсията на произволен процес е неслучайна (редовна) функция на времето, чиято стойност във всеки момент от време е равно на дисперсията на съответното напречно сечение на произволния процес.

Стандартно отклонение произволен процес е

Преди да дадем дефиниция на произволен процес, нека си припомним основните понятия от теорията на случайните променливи. Както знаете, произволна величина е величина, която в резултат на експеримент може да приеме една или друга стойност, неизвестна предварително. Правете разлика между дискретни и непрекъснати случайни променливи. Основната характеристика на произволната величина е законът на разпределението, който може да бъде определен под формата на графика или в аналитична форма. С интегрален закон за разпределение, функцията на разпределение, където е вероятността текущата стойност на произволна променлива да е по-малка от определена стойност. При диференциално разпределение се използва плътността на вероятността. Числени характеристики на случайните величини са така наречените моменти, от които най-често срещаният момент от първи ред - средната стойност (математическо очакване) на случайна променлива и централният момент от втори ред - дисперсия. Ако има няколко случайни променливи (система от случайни променливи), се въвежда концепцията за корелационен момент.

Обобщение на концепцията за случайна променлива е концепцията произволна функция, т.е. функция, която в резултат на опита може да приеме една или друга форма, неизвестна предварително. Ако аргументът на функцията е време т,тогава й се обаждат произволенили стохастичен процес.

Нарича се специфичен тип случаен процес, получен в резултат на опит изпълнениеслучаен процес и е обикновена неслучайна (детерминистична) функция. От друга страна, във фиксиран момент от времето имаме така нареченото напречно сечение на случаен процес под формата на произволна променлива.

За да се опишат случайни процеси, концепциите на теорията на случайните величини се обобщават по естествен начин. За някакъв фиксиран момент от времето произволният процес се превръща в произволна променлива, за която можете да въведете функция, наречена едномерен закон за разпределениетопроизволен процес. Законът за едномерно разпределение не е изчерпателна характеристика на случаен процес. Например, той не характеризира корелацията (връзката) между отделните участъци на произволен процес. Ако вземем две различни точки във времето и, може да се въведе двумерен закон за разпределение и т.н. В рамките на нашето по-нататъшно разглеждане ще се ограничим главно до едномерни и двумерни закони.

Помислете за най-простите характеристики на произволен процес, подобни на числените характеристики на произволна променлива. Очаквана стойностили зададено средно

и дисперсия

Математическото очакване е определена средна крива, около която се групират отделни реализации на случаен процес, а дисперсията характеризира във всеки момент от време разпространението на възможните реализации. Понякога се използва стандартно отклонение.

За да се характеризира вътрешната структура на произволен процес, се въвежда понятието корелация (автокорелация) функции

Наред с математическото очакване (средно за множеството) (3.1) се въвежда още една характеристика на случаен процес - означавапроизволен процес за отделно изпълнение (средно във времето)

За два случайни процеса може да се въведе и концепцията за кръстосана корелационна функция по аналогия с (3.3).

Един от специалните случаи на произволен процес, който се използва широко в практиката е стационарен случаен процесТова е случаен процес, чиито вероятностни характеристики не зависят от времето. Така че, за стационарен случаен процес, и корелационната функция зависи от разликата, т.е. е функция на един аргумент.

Стационарният случаен процес е до известна степен аналогичен на обикновените или стационарни процеси в системите за управление.

Стационарните стохастични процеси имат интересно свойство, наречено ергодична хипотеза... За стационарен случаен процес всяка средна стойност за множеството е равна на средната за времето. По-специално, например, това свойство често прави възможно опростяването на физическото и математическото моделиране на системи при произволни влияния.

Както е известно, при анализа на детерминирани сигнали широко се използват техните спектрални характеристики, базирани на редовете на Фурие или интеграла. Подобна концепция може да бъде въведена за случайни стационарни процеси. Разликата ще бъде, че за произволен процес амплитудите на хармоничните компоненти ще бъдат произволни, а спектърът на статичен случаен процес ще описва разпределението на вариациите върху различни честоти.

Спектрална плътностстационарен случаен процес е свързан с неговата корелационна функция чрез трансформации на Фурие:

където корелационната функция ще се интерпретира като оригинал и като изображение.

Има таблици, свързващи оригинали и изображения. Например, ако, тогава.

Нека отбележим връзката между спектралната плътност и корелационната функция с дисперсията д

Литература: [Л.1], с. 155-161

[L.2], стр. 406-416, 42-426

[L.3], стр. 80-81

Случайните процеси са математически модели на произволни сигнали и шум. Случаен процес (SP) е промяна в произволна променлива във времето... Случайните процеси включват повечето процеси, протичащи в радиотехническите устройства, както и смущения, съпътстващи предаването на сигнали по комуникационни канали. Случайни процеси могат да бъдат непрекъснато(NSP), или отделен(DSP) в зависимост от това коя случайна променлива е непрекъсната или дискретна промяна във времето. В бъдеще основният фокус ще бъде НРС.

Преди да се заемем с изследването на случайните процеси, е необходимо да се определят начините за тяхното представяне. Ще обозначим произволен процес чрез и неговото конкретно изпълнение чрез. Може да бъде представен и произволен процес набор (ансамбъл) от реализацииили един, но доста продължително изпълнение на... Ако снимате няколко осцилограма на произволен процес и поставите снимките една под друга, тогава съвкупността от тези снимки ще представлява ансамбъл от реализации (фиг. 5.3).

Ето първото, второто,..., k-то изпълнение на процеса. Ако изведем промяната на произволната променлива на лентата на записващото устройство за достатъчно дълъг интервал от време T, тогава процесът ще бъде представен от единична реализация (фиг. 5.3).

Подобно на случайните променливи, случайните процеси се описват чрез закони за разпределение и вероятностни (числови) характеристики. Вероятностните характеристики могат да бъдат получени както чрез осредняване на стойностите на произволен процес върху ансамбъл от реализации, така и чрез осредняване върху една реализация.

Нека произволен процес е представен от ансамбъл от реализации (фиг. 5.3). Ако изберем произволен момент във времето и фиксираме стойностите, взети от реализациите в този момент във времето, тогава комбинацията от тези стойности образува едномерна секция на SP

и е произволна променлива. Както вече беше подчертано по-горе, изчерпателна характеристика на произволна променлива е функцията на разпределение или едномерната плътност на вероятността

.

Естествено, и двете, и имат всички свойства на функцията на разпределение и плътността на разпределението на вероятностите, разгледани по-горе.

Числовите характеристики в разреза се определят в съответствие с изрази (5.20), (5.22), (5.24) и (5.26). Така че, по-специално, математическото очакване на съвместното предприятие в раздела се определя от израза

а дисперсия - по израза

Законите за разпределението и числените характеристики само в раздела обаче не са достатъчни, за да опишат произволен процес, който се развива във времето. Следователно е необходимо да се разгледа вторият раздел (фиг. 5.3). В този случай SP ще бъде описан от две произволни променливи и на разстояние един от друг с интервал от време и да се характеризира с двумерна функция на разпределение и двуизмерна плътност , където , . Очевидно, ако въведем третото, четвъртото и т.н. раздел, може да се стигне до многоизмерна (N-мерна) функция на разпределение и съответно до многоизмерна плътност на разпределение.

Най-важната характеристика на произволния процес е автокорелационна функция(ACF)

установяване на степента на статистическа връзка между стойностите на SP в моменти от време и

Представянето на СП под формата на ансамбъл от реализации води до концепцията за стационарност на процеса. Случайният процес е стационаренако всички начални и централни моменти са независими от времето, т.е.

, .

Това са строги условия, следователно, когато са изпълнени, се разглежда съвместното предприятие неподвижно в тесен смисъл.

На практика концепцията за стационарност се използва в широк смисъл... Случаен процес е стационарен в широк смисъл, ако неговото математическо очакване и дисперсия не зависят от времето, т.е.

а автокорелационната функция се определя само от интервала и не зависи от избора на времевата ос

По-нататък ще бъдат разгледани само случайни процеси, стационарни в широк смисъл.

По-горе беше отбелязано, че освен да бъде представен от ансамбъл от реализации, произволен процес може да бъде представен и от една реализация във времевия интервал T. Очевидно всички характеристики на процеса могат да бъдат получени чрез усредняване на стойностите на процеса. с течение на времето.

Математическото очакване на SP, когато се осредни във времето, се определя, както следва:

. (5.46)

Оттук следва физическото значение: математическото очакване е средната стойност (постоянен компонент) на процеса.

Дисперсията на съвместното предприятие се определя от израза

и има физическото значение на средната мощност на променливия компонент на процеса.

Автокорелационна функция, когато се осреднява във времето

Случайният процес се нарича ергодиченако неговите вероятностни характеристики, получени чрез осредняване по ансамбъла, съвпадат с вероятностните характеристики, получени чрез осредняване за времето на единична реализация от този ансамбъл. Ергодичните процеси са стационарни.

Използването на изрази (5.46), (5.47) и (5.48) изисква, строго погледнато, изпълнението на случаен процес с голяма (теоретично безкрайна) дължина. При решаване на практически задачи интервалът от време е ограничен. Освен това повечето процеси се считат за приблизително ергодични и вероятностните характеристики се определят в съответствие с изразите

; (5.49)

;

Наричат ​​се произволни процеси, за които математическото очакване е изключено центриран... В това, което следва, и ще означава стойностите на центрирани произволни процеси. Тогава изразите за дисперсия и автокорелационна функция приемат формата

; (5.50)

Нека отбележим свойствата на ACF на ергодичните случайни процеси:

- автокорелационната функция е реална функция на аргумента,

- автокорелационната функция е четна функция, т.е. ,

- с увеличаване, ACF намалява (не непременно монотонно) и клони към нула при,

- стойността на ACF at е равна на дисперсията (средната мощност) на процеса

.

На практика често е необходимо да се работи с две или повече смесени предприятия. Например, смес от произволен сигнал и смущения се подава едновременно към входа на радиоприемник. Връзката между два случайни процеса се установява от кръстосана корелационна функция(VKF). Ако и са два случайни процеса, характеризиращи се с реализации на и, тогава кръстосаната корелационна функция се определя от израза

Ако някаква променлива х зависи от скаларния аргумент ти за всяка фиксирана стойност на последната е произволна променлива, а след това променливата x (t)наречена случайна функция.

Ако аргументът тпроменливата x (t)е време, тогава такава случайна функция се нарича случаен процес. Например, ъгълът на наклон на самолет, движещ се в турбулентна атмосфера, е случаен процес.

Ако х-вектор, след това пристрастяване x (t)- векторен случаен процес. Например, движението на центъра на масата на самолета по траектория се характеризира с шестизмерен вектор x (t) = (x, y, z, V x, V y, V z).Ако движението на апарата се извършва под действието на случайни фактори, тогава x (t)- векторен случаен процес.

При някои експерименти се наблюдават реализации x i (t), i-1, 2, ... произволен процес х (t); и- номер на изпълнение.

Статистическо описание на случаен процес x (t)се извършват чрез разглеждане на набора от случайни променливи x 1 = x (t 1),..., x i = x (t i),съответстващи на различни времена т,взети на разглеждания интервал на неговата промяна. Смята се, че произволен случаен процес x (t)е напълно описан, ако е посочен метод за конструиране на последователност от плътности на вероятностите p (x, t); p (x 1 , т;х 2, t 2);...; p (x 1, t 1; ...; x n, t n)на, къде .

Едномерна плътност p (x, t)ви позволява да определите вероятността да ударите произволна променлива x (t)в интервала:

Използвайки двумерната плътност на ставите, се определя с каква вероятност две произволни величини х 1и х 2попадат в интервалите и съответстващи на моментите т 1и t 2:

и така за всеки П.

Плътностите на условно разпределение на вероятностите могат също да се използват за описване на случайни процеси. Условната плътност на вероятността характеризира разпределението на вероятностите на произволна променлива , изпълнението на които в момента премина през точката . По същия начин, условната плътност е плътността на разпределението на вероятностите на произволна променлива x n = x (t n),изпълнението на които в предишните моменти приемаше фиксирани стойности . Като се вземе предвид формула (1.7), следните отношения са валидни между съвместно безусловно и условно разпределение:

Наблюдават се следните ограничаващи свойства на безусловните и условните разпределения:

където е делта функцията в точката X 1.

В друг ограничаващ случай

Класификацията на случайните процеси се извършва в зависимост от свойствата, които притежават техните съвместни безусловни и условни разпределения.

Напълно случаен процес.процес x (t)се нарича абсолютно произволно, ако случайните променливи и са независими за произволно малки . Като се вземе предвид (1.10), за такъв процес получаваме, че общото n-мерно разпределение за произволно П.се определя от съотношението

т.е. абсолютно случаен процес се описва напълно от неговото едномерно разпределение p (x, i),познато на всички т.

Марков процес.Нека зададем интервала на възможна промяна на аргумента тпроизволен процес x (t)времеви редове. Случаен процес x (t)се нарича марковски, ако удовлетворява отношението за произволно .

За процес на Марков, плътността на условната вероятност на произволна променлива зависи само от това каква е била стойността на случайната променлива и по никакъв начин не зависи от това какво е било изпълнението на този процес в предишните моменти . Плътност се нарича също плътност на вероятността на прехода на процеса на Марков х (t).За процес на Марков x (t),като се вземат предвид (1.34) и (1.40), имаме се определя от предишната стойност и приращението на този интервал, независимо от нарастването на предишните интервали.

Гаусов случаен процес.Случаен процес x (t),чиято обща n-мерна плътност на вероятността за всякакви Пи всеки е гаусов, се нарича гаусов случаен процес.