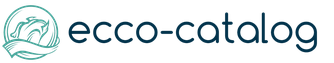Վերջին օրինակը ներկայացնում է այբբենական կարգի հայեցակարգը:

Այբուբենայբուբենի տառեր կոչվող զույգերով տարբեր նիշերի բազմություն է: Օրինակ կարելի է համարել ցանկացած եվրոպական լեզվի այբուբենը, ինչպես նաև 10 արաբական թվերի այբուբենը: Համակարգչում ստեղնաշարը և որոշ օժանդակ միջոցներ որոշում են վավեր նիշերի այբուբենը:

Բառը այբուբենովԱ -այբուբենի նիշերի բազմություն Ա.Բառը գրված է այբբենական տառերով անընդմեջ, ձախից աջ, առանց բացատների Բնական թիվը թվային այբուբենի բառ է: Բանաձևը միշտ չէ, որ բառ է նիշերի ոչ գծային դասավորության, վերնագրերի (ցուցանիշների) առկայության պատճառով: և ենթագրեր (փոփոխականների ինդեքսներ, լոգարիթմների հիմքեր) նիշեր, կոտորակային բար, նշանների ռադիկալներ և այլն; սակայն, որոշ պայմանագրերի համաձայն, այն կարող է փոխակերպվել տողի, որն օգտագործվում է, օրինակ, համակարգչային ծրագրավորման մեջ (օրինակ, աստիճանի նշանը գրվում է որպես 2 բազմապատկման նշան անընդմեջ. 5 ** 3 նշանակում է երրորդ հզորություն 5.

Լեքսիկո-գրաֆիկական (այբբենական) դասակարգում՝այբուբենի տարբեր բառերի համար՝ պատվիրված

պատվերը սահմանվում է խորհրդանիշներով՝ եթե

հնարավոր ներկայացում որտեղ կամ

(ենթաբառը կարող է դատարկ լինել), կամ - դատարկ ենթաբառ

Այս սահմանման մեջ նախածանցը (սկզբնական ենթաբառը) նույնն է երկու բառերի համար, կամ ձախ կողմում գտնվող առաջինները տարբեր են.

նիշերը, կամ - բառ-պոչի վերջին նիշը

ենթաբառեր.

Այսպիսով, բառերի այբբենական դասավորությունը որոշվում է առաջին նիշով՝ դրանք ձախից տարբերելու համար (օրինակ, KONUS բառը նախորդում է KOSINUS բառին, քանի որ դրանք առաջին անգամ տարբերվում են երրորդ տառով, իսկ H-ն նախորդում է C-ին ռուսերենում։ Այբուբեն). Համարվում է նաև, որ տիեզերական նիշը նախորդում է այբուբենի ցանկացած նիշի՝ այն դեպքում, երբ բառերից մեկը մյուսի նախածանցն է (օրինակ՝ KOH և KONUS)

Վարժությունը.Ստուգեք, որ տասնորդական նշումով նույն թվանշաններով բնական թվերի այբբենական դասավորությունը նույնն է, ինչ ըստ մեծության:

Թող Ա -մասնակի պատվիրված հավաքածու. Նյութը կոչվում է առավելագույնը v Ա,եթե չկա տարր, որի համար ա< b. Տարր ականչեց մեծագույն v Ա,եթե այլ բանի համար, քան ատարրն ավարտված է Բ<а-

Սիմետրիկորեն սահմանված նվազագույն և ամենափոքրտարրեր. Ամենամեծ և առավելագույն (համապատասխանաբար՝ ամենափոքր և նվազագույն) տարրերի հասկացությունները տարբեր են՝ տես. Տես օրինակը Նկար 14-ում: Հավաքածուն նկ. 14, և ունի ամենամեծ տարրը Ռ,այն նաև առավելագույնն է, կա երկու նվազագույն տարր. s և t,ամենափոքրը չկա: Նկար 14-ում, բ, ընդհակառակը, երկու առավելագույն տարրերով հավաքածու / և ժ,չկա ամենամեծը, նվազագույնը, այն նաև ամենափոքրն է՝ մեկը. Տ.

Ընդհանուր առմամբ, եթե հավաքածուն ունի ամենամեծ (համապատասխանաբար, ամենափոքր) տարրը, ապա միայն մեկը (կարող է և չկա):

Կարող են լինել մի քանի առավելագույն և նվազագույն տարրեր (կարող է ընդհանրապես չլինել՝ անսահման հավաքածուում, վերջնական դեպքում՝ պետք է լինի)։

Դիտարկենք ևս երկու օրինակ։ - հարաբերություն նկարահանման հրապարակում Ն:

«Յբաժանում է X»,կամ «Xթվի բաժանարար է Y"(Օրինակ,

) ռեֆլեքսիվ է և անցողիկ։ Դիտարկենք այն 30-ի բաժանարարների վերջավոր բազմության վրա:

Հարաբերությունը մասնակի կարգի (ոչ խիստ) հարաբերություն է

և ներկայացված է 8 կարգի հետևյալ մատրիցով, որը պարունակում է 31 նիշ

8 գագաթներով համապատասխան սխեման պետք է պարունակի 31 կապոց: ... Այնուամենայնիվ, ավելի հեշտ կլինի դիտել, եթե բացառեք 8-ը

կապան-օղակներ, որոնք պատկերում են կապի (մատրիցի անկյունագծային տարրեր) և անցողիկ կապանների ռեֆլեքսիվությունը, այսինքն. կապաններ

Եթե ​​կա Z միջանկյալ թիվ, որ

(օրինակ, մի փունջ, քանի որ): Այնուհետեւ սխեմայով

կմնան 12 կապաններ (նկ. 15); բացակայող օղակները նկատի ունեն «անցանելիություն»: 1 թիվը ամենափոքրն է, իսկ 30 թիվը

մեջ ամենամեծ տարրերը. Եթե ​​30 թվից բացառենք և

հաշվի առեք նույն մասնակի պատվիրումը նկարահանման հրապարակում, ապա

Չկա ամենամեծ տարրը, բայց կա 3 առավելագույն տարր՝ 6, 10, 15

Հիմա եկեք կառուցենք նույն սխեման Բուլյան հարաբերությունների համար

(բոլոր ենթաբազմությունների բազմությունը) երեք տարրերից բաղկացած բազմության

Պարունակում է 8 տարր.

Ստուգեք, եթե համապատասխանում եք տարրերին ա, բ, գ,համապատասխանաբար 2, 3, 5 թվերը, իսկ բազմությունները համակցելու գործողությունը համապատասխան թվերի բազմապատկումն է (այսինքն, օրինակ, ենթաբազմությունը համապատասխանում է.

արտադրյալ 2 5 = 10), ապա հարաբերակցության մատրիցը կլինի նույնը

նույնը, ինչ հարաբերությունների համար; այս երկու հարաբերությունների դիագրամները նկարագրվածի հետ

Օղակների և անցումային միացումների չեղարկումները համընկնում են մինչև նշումը (տես նկ. 16): Ամենափոքր տարրն է

Եվ ամենամեծը -

Երկուական հարաբերություններ Ռնկարահանման հրապարակում Աև Սնկարահանման հրապարակում Վկոչվում են իզոմորֆ,եթե միջեւ Ա և Բհնարավոր է սահմանել մեկ առ մեկ նամակագրություն Г, որում, եթե (այսինքն.

տարրերը փոխկապակցված են Ռ),հետո (պատկերներ

այս տարրերը փոխկապակցված են Ս).

Այսպիսով, մասամբ դասավորված բազմություններ և իզոմորֆ են:

Դիտարկված օրինակը կարելի է ընդհանրացնել։

Բուլյան հարաբերությունը մասնակի կարգ է: Եթե

Նրանք. մի փունջ Եպարունակում է Պտարրեր, ապա յուրաքանչյուրը

ենթաբազմությունը համապատասխանում է Պ-ծավալային վեկտոր հետ

բաղադրիչներ, որտեղ է բնորոշ ֆունկցիան

A / բազմության. Բոլոր նման վեկտորների հավաքածուն կարելի է դիտել որպես կետերի հավաքածու Պ- 0 կամ 1 կոորդինատներով ծավալային թվաբանական տարածություն, կամ այլ կերպ ասած՝ որպես գագաթներ Պ- ծավալային

միավոր խորանարդ, որը նշվում է, այսինքն. միավորի երկարության եզրերով խորանարդ: Համար n =Նշված 1, 2, 3 կետերը համապատասխանաբար ներկայացնում են հատվածի ծայրերը, քառակուսու գագաթները և խորանարդը, հետևաբար ընդհանուր անվանումը: / 7 = 4-ի համար, այս հարաբերակցության գրաֆիկական ներկայացումը Նկար 17-ում է: Համապատասխան

ենթաբազմություն 4 տարրից բաղկացած հավաքածուից և քառաչափից

վեկտոր, որը ներկայացնում է այս ենթաբազմության բնորոշ գործառույթը: Այն գագաթները, որոնք համապատասխանում են ենթաբազմություններին, որոնք տարբերվում են հենց մեկ տարրի առկայությամբ, միացված են միմյանց։

Նկար 17-ում քառաչափ խորանարդ է պատկերված այնպես, որ մեկի վրա

մակարդակը պարունակում է զույգ անհամեմատելի տարրեր, որոնք պարունակում են նույն թվով միավորներ գրառումներում (0-ից մինչև 4), կամ, այլ կերպ ասած, նույն թվով տարրեր ներկայացված ենթաբազմություններում:

Նկար 18ա, բ - 4-չափ խորանարդի այլ տեսողական պատկերներ;

18ա-ում առաջին փոփոխականի առանցքը Օհուղղված դեպի վեր (ուղղահայացից դիտավորյալ շեղում, որպեսզի խորանարդի տարբեր եզրերը չմիաձուլվեն).

այս դեպքում համապատասխան եռաչափ ենթախորան X= 0-ը գտնվում է ներքևում, և համար X= 1 - ավելի բարձր: Նկ. 186 նույն առանցքը Օհուղղված խորանարդի ներսից դեպի դուրս, ներքին ենթախորանին համապատասխանում է X= O, և արտաքին - X = 1.

Վ
Նյութի ֆայլը պարունակում է 5-չափ միավոր խորանարդի պատկեր (էջ 134):

Հարաբերությունների հատկություններ.

1) ռեֆլեքսիվություն;

2) համաչափություն;

3) անցողականություն.

4) կապվածություն.

Վերաբերմունք Ռնկարահանման հրապարակում Xկանչեց արտացոլող,եթե հավաքածուի յուրաքանչյուր տարրի մասին Xկարելի է ասել, որ նա հարաբերությունների մեջ է ՌԻնքս ինձ հետ. XRx.Եթե ​​հարաբերությունը ռեֆլեքսային է, ապա գրաֆիկի յուրաքանչյուր գագաթում կա օղակ: Ընդհակառակը, գրաֆիկը, որի յուրաքանչյուր գագաթը պարունակում է օղակ, ռեֆլեքսային հարաբերությունների գրաֆիկ է:

Ռեֆլեքսիվ հարաբերությունների օրինակներ են բնական թվերի բազմության վրա «բազմակի» հարաբերակցությունը (յուրաքանչյուր թիվ իր բազմապատիկն է), և եռանկյունների նմանության հարաբերակցությունը (յուրաքանչյուր եռանկյուն իրեն նման է) և «հավասարության» հարաբերությունը։ (յուրաքանչյուր թիվ հավասար է ինքն իրեն) և այլն:

Կան հարաբերություններ, որոնք չունեն ռեֆլեկտիվության հատկություն, օրինակ՝ հատվածների ուղղահայացության հարաբերակցությունը. աբ, բա(չկա մի ուղիղ հատված, որի մասին կարող ենք ասել, որ այն ուղղահայաց է իրեն) . Հետևաբար, այս հարաբերության գրաֆիկի վրա մեկ օղակ չկա:

Այն չունի ռեֆլեքսիվության հատկություն և հատվածների համար հարաբերակցությունը «ավելի երկար» է, բնական թվերի համար՝ «ավելի 2-ով» և այլն։

Վերաբերմունք Ռնկարահանման հրապարակում Xկանչեց հակառեֆլեկտիվեթե հավաքածուից որևէ տարրի համար Xմիշտ կեղծ XRx: .

Կան հարաբերություններ, որոնք ոչ արտացոլող են, ոչ հակառեֆլեկտիվ: Նման հարաբերությունների օրինակ է կետը Xսիմետրիկ է կետին ժամըհամեմատաբար ուղիղ լ»Սահմանված է ինքնաթիռի կետերի վրա: Իրոք, գծի բոլոր կետերը լսիմետրիկ են իրենց նկատմամբ, և կետերը, որոնք չեն գտնվում ուղիղ գծի վրա լ,իրենք սիմետրիկ չեն:

Վերաբերմունք Ռնկարահանման հրապարակում Xկանչեց սիմետրիկ, եթե պայմանը բավարարված է՝ այն բանից, որ տարրը Xկապված է տարրի հետ y, հետևում է, որ տարրը yհարաբերության մեջ է Ռտարրով X:xRyyRx.

Սիմետրիկ հարաբերությունների գրաֆիկն ունի հետևյալ հատկանիշը. յուրաքանչյուր սլաքի հետ միասին XԴեպի y, գրաֆիկը պարունակում է սլաք, որը գնում է yԴեպի X(նկ. 35):

Սիմետրիկ հարաբերությունների օրինակներ կարող են լինել հետևյալը՝ հատվածների «զուգահեռության» հարաբերակցությունը, հատվածների «ուղղահայության» հարաբերակցությունը, հատվածների «հավասարության» հարաբերակցությունը, եռանկյունների նմանության հարաբերակցությունը, «հավասարության» հարաբերակցությունը։ կոտորակների և այլն:

Կան հարաբերություններ, որոնք չունեն համաչափության հատկություն։

Իսկապես, եթե հատվածը Xավելի երկար, քան հատվածը ժամը, ապա հատվածը ժամըչի կարող լինել ավելի երկար, քան հատվածը X... Այս հարաբերության գրաֆիկն ունի մի յուրահատկություն՝ գագաթները միացնող սլաքն ուղղված է միայն մեկ ուղղությամբ։

Վերաբերմունք Ռկոչվում են հակասիմետրիկեթե որևէ տարրի համար Xև yճշմարտության xRyհետևում է կեղծիքը yRx:: xRyyRx.

Բացի «ավելի երկար» հարաբերությունից, հատվածների բազմության վրա կան նաև այլ հակասիմետրիկ հարաբերություններ: Օրինակ, թվերի համար «ավելի մեծ» հարաբերակցությունը (եթե Xավելին ժամը, ապա ժամըավելին չի կարող լինել X), «ավելի շատ» հարաբերակցությունը և այլն:

Կան հարաբերություններ, որոնք չունեն ո՛չ համաչափության հատկություն, ո՛չ էլ հակահամաչափության հատկություն։

R հարաբերությունը նկարահանման հրապարակում Xկոչվում են անցումային,եթե ինչ տարրից Xհարաբերության մեջ է Ռտարրով y,և տարր yհարաբերության մեջ է Ռտարրով զ, հետևում է, որ տարրը Xհարաբերության մեջ է Ռտարրով զ: xRyև yRzxRz.

Անցումային հարաբերությունների գծապատկեր՝ յուրաքանչյուր զույգ սլաքներով XԴեպի yև սկսած yԴեպի զ, պարունակում է սլաք, որը գնում է XԴեպի զ.

Անցումային հատկություն ունի նաև հատվածների բազմության վրա «ավելի երկար» կապը. եթե հատվածը աավելի երկար, քան հատվածը բ, Բաժին բավելի երկար, քան հատվածը Հետ, ապա հատվածը աավելի երկար, քան հատվածը Հետ.Հատվածների բազմության վրա «հավասարություն» կապն ունի նաև անցողիկ հատկություն. (a =b, b = c) (a = c).

Կան հարաբերություններ, որոնք չունեն անցողիկության հատկություն։ Նման հարաբերություն է, օրինակ, ուղղահայացության հարաբերակցությունը. եթե հատվածը ահատվածին ուղղահայաց բ, և հատվածը բհատվածին ուղղահայաց Հետ, ապա հատվածները աև Հետոչ ուղղահայաց!

Գոյություն ունի հարաբերությունների մեկ այլ հատկություն, որը կոչվում է կապվածության հատկություն, իսկ այն տիրապետող հարաբերությունը կոչվում է կապված։

Վերաբերմունք Ռնկարահանման հրապարակում Xկանչեց կապված,եթե որևէ տարրի համար Xև yայս հավաքածուից բավարարվում է հետևյալ պայմանը՝ եթե Xև yտարբեր են, ապա կամ Xհարաբերության մեջ է Ռտարրով y, կամ տարր yհարաբերության մեջ է Ռտարրով X... Օգտագործելով սիմվոլներ, այն կարելի է գրել այսպես. xyxRyկամ yRx.

Օրինակ, բնական թվերի համար «ավելին» կապը կապակցվելու հատկություն ունի. ցանկացած տարբեր x և y թվերի համար կարելի է պնդել. x> yկամ y> x.

Կապակցված հարաբերությունների գրաֆիկի ցանկացած երկու գագաթներ միացված են սլաքով: Ճիշտ է նաև հակառակը.

Կան հարաբերություններ, որոնք կապված չեն: Նման հարաբերություն, օրինակ, բնական թվերի բազմության վրա բաժանելիության կապն է. կարող եք այդպիսի թվեր անվանել x և. yոր ոչ մի թիվ Xբաժանարար չէ yոչ էլ համար yբաժանարար չէ X(համարներ 17 և 11 , 3 և 10 և այլն) .

Դիտարկենք մի քանի օրինակ։ Նկարահանման հրապարակում X = (1, 2, 4, 8, 12)հարաբերությունը «թիվ Xթվի բազմապատիկ y«. Կառուցենք այս հարաբերության գրաֆիկը և ձևակերպենք դրա հատկությունները։

Կոտորակների հավասարության հարաբերությունն ասում են, որ համարժեք հարաբերություն է:

Վերաբերմունք Ռնկարահանման հրապարակում Xկանչեց համարժեքության հարաբերություն,եթե այն միաժամանակ տիրապետում է ռեֆլեքսիվության, համաչափության և անցողիկության հատկությանը։

Համարժեքության հարաբերությունների օրինակներ են՝ երկրաչափական պատկերների հավասարության հարաբերությունները, ուղիղների զուգահեռության հարաբերակցությունը (պայմանով, որ համընկնող ուղիղները համարվում են զուգահեռ)։

Վերը դիտարկված «կոտորակների հավասարության» առնչությամբ բազմությունը Xբաժանված է երեք ենթաբազմության. ; ; }, {; } , (). Այս ենթաբազմությունները չեն հատվում, և դրանց միավորումը համընկնում է բազմության հետ X, այսինքն. մենք ունենք հավաքածուի բաժանում դասերի:

Այսպիսով, եթե X բազմության վրա տրված է համարժեքության հարաբերություն, ապա այն առաջացնում է այս բազմության բաժանումը զույգ-անջատված ենթաբազմությունների՝ համարժեքության դասերի:

Այսպիսով, մենք սահմանել ենք, որ հավասարության հարաբերությունը հավաքածուի վրա
X= (;;;;;) համապատասխանում է այս բազմության բաժանմանը համարժեքության դասերի, որոնցից յուրաքանչյուրը բաղկացած է հավասար կոտորակներից:

Բազմաթիվը դասերի բաժանելու սկզբունքը՝ օգտագործելով համարժեքության որոշակի կապ, մաթեմատիկայի կարևոր սկզբունք է։ Ինչո՞ւ։

Նախ, համարժեք նշանակում է համարժեք, փոխարինելի: Հետևաբար, նույն համարժեքության դասի տարրերը փոխարինելի են: Այսպիսով, միևնույն համարժեքության դասի կոտորակները (;;), հավասարության հարաբերությամբ չեն տարբերվում, իսկ կոտորակը կարելի է փոխարինել մեկ այլով, օրինակ . Եվ այս փոխարինումը չի փոխի հաշվարկի արդյունքը։

Երկրորդ, քանի որ համարժեքության դասում կան տարրեր, որոնք չեն տարբերվում ինչ-որ հարաբերության տեսանկյունից, ենթադրվում է, որ համարժեքության դասը որոշվում է նրա որևէ ներկայացուցիչի կողմից, այսինքն. դասի կամայական տարր: Այսպիսով, հավասար կոտորակների ցանկացած դաս կարելի է նշել՝ նշելով այս դասին պատկանող ցանկացած կոտորակ: մեկ ներկայացուցչի կողմից համարժեքության դասը թույլ է տալիս բազմության բոլոր տարրերի փոխարեն ուսումնասիրել համարժեք դասերի ներկայացուցիչների ամբողջությունը: Օրինակ, բազմանկյունների բազմության վրա սահմանված «ունեն նույն թվով գագաթներ» համարժեքության կապը առաջացնում է այս բազմության բաժանումը եռանկյունների, քառանկյունների, հնգանկյունների և այլնի դասերի: Որոշակի դասին բնորոշ հատկությունները դիտարկվում են նրա ներկայացուցիչներից մեկի վրա:

Երրորդ, բազմությունը դասերի բաժանելը` օգտագործելով համարժեքության կապը, օգտագործվում է նոր հասկացություններ ներմուծելու համար: Օրինակ, «գծերի փաթեթ» հասկացությունը կարող է սահմանվել որպես մի ընդհանուր բան, որը զուգահեռ գծերն ունեն միմյանց հետ:

Հարաբերությունների մեկ այլ կարևոր տեսակ է պատվերի հարաբերությունը: Մտածեք խնդիրը: Նկարահանման հրապարակում X={3, 4, 5, 6, 7, 8, 9, 10 ) հարաբերությունը «ունեն նույն մնացորդը, երբ բաժանվում են 3 «. Այս հարաբերությունը ստեղծում է բազմության բաժանում Xդասերի. բոլոր թվերը բաժանվելու են մեկի 3 մնացածը 0 (սրանք թվեր են 3, 6, 9 ): Երկրորդը պարունակում է թվեր, երբ բաժանվում է 3 մնացածն է 1 (սրանք թվեր են 4, 7, 10 ): Երրորդը կպարունակի բոլոր թվերը, երբ բաժանվում է 3 մնացածն է 2 (սրանք թվեր են 5, 8 ): Իրոք, ստացված բազմությունները չեն հատվում, և դրանց միացումը համընկնում է բազմության հետ X... Հետևաբար, հարաբերությունը «ունեն նույն մնացորդը, երբ բաժանվում են 3 »Սահմանված է նկարահանման հրապարակում X, համարժեքության հարաբերություն է։

Մեկ այլ օրինակ վերցնելու համար դասարանի աշակերտների հավաքածուն կարելի է պատվիրել ըստ հասակի կամ տարիքի: Նկատի ունեցեք, որ այս կապն ունի հակասիմետրիկության և անցողիկության հատկություններ։ Կամ բոլորը գիտեն այբուբենի տառերի հերթականությունը։ Դա նախատեսված է «պետք է» հարաբերությամբ։

Վերաբերմունք Ռնկարահանման հրապարակում Xկանչեց խիստ կարգեթե այն միաժամանակ տիրապետում է հակասիմետրիկության և անցողիկության հատկություններին: Օրինակ, հարաբերությունը « X< y».

Եթե ​​հարաբերությունն ունի ռեֆլեքսիվության, հակասիմետրիկության և անցողիկության հատկություններ, ապա դա կլինի ազատ կարգը... Օրինակ, հարաբերությունը « Xy».

Կարգի հարաբերությունների օրինակներ են՝ «պակաս» հարաբերակցությունը բնական թվերի բազմության վրա, «ավելի կարճ» հարաբերակցությունը հատվածների բազմության վրա։ Եթե ​​կարգի հարաբերությունն էլ կապակցվելու հատկություն ունի, ուրեմն ասում են, որ կա գծային կարգի հարաբերություն... Օրինակ՝ «պակաս» հարաբերակցությունը բնական թվերի բազմության վրա։

Մի փունջ Xկանչեց կարգուկանոն,եթե դրա վրա նշված է պատվերի հարաբերություն:

Օրինակ, հավաքածուն X ={2, 8, 12, 32 ) կարելի է պատվիրել՝ օգտագործելով «պակաս» կապը (նկ. 41), իսկ դա կարելի է անել՝ օգտագործելով «բազմապատիկ» հարաբերությունները (նկ. 42): Բայց, լինելով կարգի հարաբերություն, «պակաս» և «բազմակի» հարաբերությունները բնական թվերի բազմությունը կարգում են տարբեր ձևերով։ «Ավելի քիչ» հարաբերակցությունը թույլ է տալիս համեմատել հավաքածուից ցանկացած երկու թվեր X, իսկ «բազմակի» հարաբերակցությունը նման հատկություն չունի։ Այսպիսով, մի երկու թիվ 8 և 12 «բազմապատիկ» հարաբերությունը կապված չէ. այդպես չի կարելի ասել 8 բազմապատիկ 12 կամ 12 բազմապատիկ 8.

Չի կարելի մտածել, որ բոլոր հարաբերությունները բաժանվում են համարժեք հարաբերությունների և կարգի հարաբերությունների։ Հսկայական թվով հարաբերություններ կան, որոնք ոչ համարժեք հարաբերություններ են, ոչ էլ կարգի հարաբերություններ։

Թող R լինի երկուական հարաբերություն A բազմության վրա:

ՍԱՀՄԱՆՈՒՄ. A բազմության վրա երկուական R կապը կոչվում է կարգի հարաբերություն A-ի վրա կամ կարգը A-ի վրա, եթե այն անցողիկ է և հակասիմետրիկ:

ՍԱՀՄԱՆՈՒՄ. R կարգի հարաբերությունը A բազմության վրա կոչվում է ոչ խիստ, եթե այն արտացոլող է A-ի վրա, այսինքն՝ A-ից որևէ մեկի համար:

R կարգի կապը կոչվում է խիստ (A-ի վրա), եթե այն հակառեֆլեքսիվ է A-ի վրա, այսինքն՝ A-ից որևէ մեկի համար: Այնուամենայնիվ, անցումային R հարաբերության հակառեֆլեքսիվությունը ենթադրում է, որ այն հակասիմետրիկ է: Հետևաբար, կարելի է տալ հետևյալ համարժեք սահմանումը.

ՍԱՀՄԱՆՈՒՄ. A բազմության վրա երկուական R հարաբերությունը կոչվում է խիստ կարգ A-ի վրա, եթե այն անցողիկ է և հակառեֆլեքսիվ A-ի վրա:

Օրինակներ. 1. Թող M բազմության բոլոր ենթաբազմությունների բազմությունը լինի:

2. Իրական թվերի բազմության հարաբերությունները, համապատասխանաբար, խիստ և ոչ խիստ կարգի հարաբերություններն են։

3. Բնական թվերի բազմության մեջ բաժանելիության կապը ոչ խիստ կարգի հարաբերություն է։

ՍԱՀՄԱՆՈՒՄ. A բազմության վրա երկուական R հարաբերությունը կոչվում է նախադասային հարաբերություն կամ A-ի նախադասային հարաբերություն, եթե այն ռեֆլեքսիվ է և անցումային:

Օրինակներ. 1. Ամբողջ թվերի բազմության մեջ բաժանելիության կապը կարգ չէ։ Այնուամենայնիվ, այն ռեֆլեքսիվ է և անցողիկ, ինչը նշանակում է, որ դա նախնական պատվեր է:

2. Տրամաբանական հետևանք հարաբերությունը նախադրյալ տրամաբանական բանաձևերի բազմության նախնական պատվեր է:

Գծային կարգը. Պատվիրելու կարևոր հատուկ դեպքը գծային պատվիրումն է:

ՍԱՀՄԱՆՈՒՄ. Բազմության վրա կարգի հարաբերությունը կոչվում է գծային կարգի հարաբերություն կամ գծային կարգ, եթե այն միացված է, այսինքն՝ A-ից ցանկացած x, y-ի համար:

Պատվերային հարաբերությունը, որը գծային չէ, սովորաբար կոչվում է մասնակի պատվեր կամ մասնակի դասավորություն:

Օրինակներ. 1. Իրական թվերի բազմության «պակաս» հարաբերակցությունը գծային կարգի հարաբերություն է։

2. Ռուսաց լեզվի բառարաններում ընդունված կարգի հարաբերությունը կոչվում է բառարանագրական։ Ռուսաց լեզվի բառերի բազմության բառարանագրական կարգը գծային կարգ է։

«Պատվեր» բառը հաճախ օգտագործվում է ամենատարբեր հարցերում: Սպան հրաման է տալիս. «Հաշվի՛ր թվերի հերթականությամբ», թվաբանական գործողությունները կատարվում են որոշակի հերթականությամբ, մարզիկները դառնում են հասակի, բոլոր առաջատար շախմատիստները դասավորվում են որոշակի հերթականությամբ՝ այսպես կոչված Էլոյի գործակիցներով (ամերիկացի պրոֆեսոր. ով մշակել է համակարգի գործակիցները, որոնք թույլ են տալիս հաշվի առնել խաղացողների բոլոր հաջողություններն ու անհաջողությունները), առաջնությունից հետո բոլոր ֆուտբոլային թիմերը դասավորվում են որոշակի հերթականությամբ և այլն։ մաս, բառի կարգը նախադասության մեջ (փորձեք հասկանալ, թե ինչ է նախադասությունը «որովհետև նա ծեր մարդ է, ես էշը չեմ դրել»):

Կոմպլեկտի տարրերը մեկը մյուսի հետևից դասավորելով՝ մենք դրանով պատվիրում ենք դրանք կամ ինչ-որ առնչություն ենք հաստատում նրանց միջև։ որպեսզի.Ամենապարզ օրինակը բնական թվերի բնական դասավորությունն է։ Դրա բնականությունը կայանում է նրանում, որ ցանկացած երկու բնական թվի համար մենք գիտենք, թե դրանցից որն է հաջորդում մյուսին կամ նրանցից որն է մյուսից մեծ, այնպես որ կարող ենք բնական թվերը դասավորել հաջորդականությամբ, որպեսզի ավելի մեծ թիվը գտնվի. օրինակ՝ փոքրից աջ՝ 1, 2, 3, .... Իհարկե, տարրերի հաջորդականությունը կարելի է գրել ցանկացած ուղղությամբ, ոչ միայն ձախից աջ: Բնական թվերի հենց հայեցակարգն արդեն իսկ պարունակում է դասակարգման գաղափար: Սահմանելով բազմության տարրերի որոշ հարաբերական դասավորություն՝ մենք դրանով իսկ դրա վրա դնում ենք երկուական կարգի հարաբերություն, որը յուրաքանչյուր կոնկրետ դեպքում կարող է ունենալ իր անունը, օրինակ՝ «պակաս լինել», «ավելի մեծ», «մինչև պարունակել «», հետևել հետո «-ում և այլն: Կարգի նշանները կարող են լինել նաև տարբեր, օրինակ՝ Í և այլն:

Պատվերի հարաբերության հիմնական տարբերակիչ հատկանիշը նրա անցողիկ հատկությունն է։ Այսպիսով, եթե գործ ունենք որոշ օբյեկտների հաջորդականության հետ x 1, x 2, ..., x n,..., հրամայեց, օրինակ, առնչությամբ, ապա այն, ինչ կատարվում է x 1x 2... x n..., դա պետք է հետևի ցանկացած զույգի համար x i, x jկատարվում են նաև այս հաջորդականության տարրեր x ix j:

Մի զույգ տարրերի համար x iժհարաբերությունների գրաֆիկում վերևից սլաք ենք գծում x iդեպի բարձրունք x j, այսինքն՝ ամենափոքր տարրից մինչև ամենամեծը։

Պատվերի հարաբերությունների գրաֆիկը կարելի է պարզեցնել՝ օգտագործելով այսպես կոչված մեթոդը Hasse դիագրամներ. Hasse դիագրամը կառուցված է հետևյալ կերպ. Ավելի փոքր տարրերը տեղադրվում են ավելի ցածր կարգով, իսկ մեծերը՝ ավելի բարձր: Քանի որ նման կանոններից մեկը բավարար չէ նկարի համար, գծեր են գծվում՝ ցույց տալու համար, թե երկու տարրերից որն է ավելի մեծ և որը փոքր, քան մյուսը: Այս դեպքում բավական է միայն իրար հաջորդող տարրերի գծեր գծել։ Hasse-ի դիագրամների օրինակները ներկայացված են նկարում.

Hasse դիագրամում սլաքները կարող են բաց թողնել: Hasse դիագրամը կարող է պտտվել հարթության մեջ, բայց ոչ կամայական: Շրջելիս անհրաժեշտ է պահպանել դիագրամի գագաթների հարաբերական դիրքը (վերևում - ներքևում).

Վերաբերմունք Ռհավաքածուի մեջ Xկանչեց խիստ կարգուկանոնի վերաբերմունք,եթե այն անցողիկ է և ասիմետրիկ:

Այն բազմությունը, որում սահմանված է խիստ կարգի կապը, կոչվում է կարգուկանոն.Օրինակ՝ բնական թվերի բազմությունը դասավորված է «պակաս» հարաբերակցությամբ։ Բայց նույն բազմությունը պատվիրված է մեկ այլ առնչությամբ՝ «բաժանելի է» և «ավելին»:

Բնական թվերի բազմության մեջ «պակաս» հարաբերությունների գրաֆիկը կարելի է պատկերել որպես ճառագայթ.

Վերաբերմունք Ռ v Xկոչվում է հարաբերություններ ոչ խիստ (մասնակի) կարգեթե այն անցողիկ է և հակասիմետրիկ։ Ցածր կարգի ցանկացած հարաբերություն ռեֆլեքսիվ է:

«Մասամբ» էպիտետն արտահայտում է այն փաստը, որ այս առումով, թերեւս, ոչ բոլոր տարրերն են համադրելի։

Մասնակի կարգի հարաբերությունների տիպիկ օրինակները ոչ ավելի, ոչ պակաս, ոչ ավելի հին են: Հարաբերությունների անվանումներում «ոչ» մասնիկը ծառայում է արտահայտելու դրանց ռեֆլեքսիվությունը։ «Ոչ ավելին» հարաբերակցությունը համընկնում է «պակաս կամ հավասար» հարաբերության հետ, իսկ «ոչ պակաս» հարաբերությունը նույնն է, ինչ «ավելի կամ հավասար»։ Այս առումով մասնակի կարգը նույնպես կոչվում է ոչ խիստպատվեր. Հաճախ մասնակի (ոչ խիստ) կարգի հարաբերությունը նշվում է «» նշանով։

Բազմության ենթաբազմությունների միջև Í ներառման կապը նույնպես մասնակի կարգ է: Ակնհայտ է, որ ոչ ամեն երկու ենթաբազմություններն են համեմատելի այս առնչությամբ: Ստորև բերված նկարը ցույց է տալիս բազմության բոլոր ենթաբազմությունների բազմության վրա ներառման մասնակի կարգը (1,2,3): Գրաֆիկի վրա գտնվող սլաքները, որոնք պետք է ուղղված լինեն դեպի վեր, ցուցադրված չեն:

Այն բազմությունները, որոնց վրա տրված է մասնակի հրամանը, կոչվում են մասնակի պատվիրված,կամ պարզապես կարգուկանոնհավաքածուներ.

Տարրերը Xև ժամըկոչվում են մասնակի պատվիրված հավաքածու համեմատելեթե Xժամըկամ ժամըX.Հակառակ դեպքում դրանք համեմատելի չեն։

Կարգավորված բազմությունը, որտեղ ցանկացած երկու տարր համեմատելի են, կոչվում է գծային կարգովիսկ կարգը գծային է։ Գծային կարգը կոչվում է նաև կատարյալ կարգ։

Օրինակ՝ բնական կարգով բոլոր իրական թվերի բազմությունը, ինչպես նաև նրա բոլոր ենթաբազմությունները գծային են դասավորված։

Կարելի է պատվիրել ամենատարբեր բնույթի առարկաներ հիերարխիկորեն։Ահա մի քանի օրինակներ.

Օրինակ 1. Գրքի մասերը դասավորված են այնպես, որ գիրքը պարունակում է գլուխներ, գլուխները՝ բաժիններ, իսկ բաժինները՝ ենթաբաժիններ:

Օրինակ 2 Համակարգչի ֆայլային համակարգում թղթապանակները գտնվում են միմյանց մեջ՝ կազմելով ճյուղավորվող կառուցվածք:

Օրինակ 3. Ծնող-երեխա հարաբերությունները կարելի է պատկերել այսպես կոչված տոհմածառ,որը ցույց է տալիս, թե ով ում նախահայրն է (կամ սերունդը):

Թող նկարահանման հրապարակում Ատրված է մասնակի պատվեր. Տարր Xկանչեց առավելագույն (նվազագույն) A բազմության տարրը, եթե այն փաստից, որ Xժամը(ժամըX),հետևում է հավասարությունը X= ժամը.Այսինքն՝ տարրը Xառավելագույնն է (նվազագույնը), եթե ցանկացած տարրի համար ժամըկամ դա ճիշտ չէ Xժամը(ժամըX), կամ X=ժամը.Այսպիսով, առավելագույն (նվազագույն) տարրը ավելի մեծ է (պակաս), քան բոլոր այն տարրերը, որոնց հետ այն կապված է:

Տարր Xկանչեց ամենամեծ (ամենափոքր),եթե որևէ մեկի համար ժամըÎ Ակատարվեց ժամը< х (х< у).

Մասամբ պատվիրված հավաքածուն կարող է ունենալ մի քանի նվազագույն և/կամ առավելագույն տարրեր, բայց չի կարող լինել մեկից ավելի ամենափոքր և ամենամեծ տարրը: Ամենափոքր (ամենամեծ) տարրը և նվազագույնն է (առավելագույնը), բայց հակառակը ճիշտ չէ: Ձախ կողմի նկարը ցույց է տալիս մասնակի կարգ երկու նվազագույն և երկու առավելագույն տարրերով, իսկ աջ կողմում՝ մասնակի կարգ՝ ամենափոքր և ամենամեծ տարրերով.

Վերջնական մասամբ պատվիրված հավաքածուում միշտ լինում են նվազագույն և առավելագույն տարրեր:

Պատվիրված հավաքածուն, որն ունի ամենամեծ և ամենափոքր տարրերը կոչվում է սահմանափակված.Նկարը ցույց է տալիս անսահման սահմանափակ բազմության օրինակ: Իհարկե, դուք չեք կարող պատկերել անսահման հավաքածու վերջնական էջում, բայց կարող եք ցույց տալ դրա կառուցման սկզբունքը: Գագաթների մոտ գտնվող օղակները այստեղ ցուցադրված չեն պարզության համար: Նույն պատճառով, անցողիկության հատկությունը ցուցադրելու համար ոչ մի աղեղ չի ցուցադրվում: Այլ կերպ ասած, նկարը ցույց է տալիս պատվերի հարաբերությունների Hasse դիագրամը:

Անսահման հավաքածուները կարող են չունենալ առավելագույնը կամ նվազագույնը, կամ երկուսն էլ: Օրինակ՝ բնական թվերի բազմությունը (1,2, 3, ...) ունի ամենափոքր տարրը՝ 1, բայց չունի առավելագույնը։ Բնական կարգով բոլոր իրական թվերի բազմությունը չունի ոչ ամենափոքր, ոչ էլ ամենամեծ տարրը: Այնուամենայնիվ, նրա ենթաբազմությունը բաղկացած է բոլոր թվերից X< 5, ունի ամենամեծ տարրը (թիվ 5), բայց չունի ամենափոքրը:

2) X բազմության հարաբերությունը կոչվում է հարաբերություն խստորեն պատվիրելեթե այն հակասիմետրիկ է և անցողիկ: Հարաբերությունները կոչվում են հակասիմետրիկեթե a-ն b-ի հետ կապված է, չի նշանակում, որ b-ը a-ի հետ է կապված (a, b ∈ X և R-ը → R-ում a) Ռ - հարաբերությունների մեջ լինել:Հարաբերությունները կոչվում են անցողիկ, եթե որևէ տարրի համար a, b, c այն փաստից, որ a R-ն և R-ում c → որ a R c, a, b, c ∈ X: Օրինակ՝ «ավելի, պակաս» հարաբերակցությունը: Այն բազմությունը, որի վրա նշված է խիստ պատվերային հարաբերությունը, կոչվում է կարգուկանոնշատ.

3) X բազմության հարաբերությունը կոչվում է հարաբերություն ոչ խիստ հրամանեթե այն ռեֆլեկտիվ է, ասիմետրիկ և անցողիկ: Օրինակ՝ հարաբերակցությունը ≥ ≤: Եթե ​​պատվերի հարաբերությունն ունի կապի հատկություն, ապա ասում են, որ դա հարաբերություն է գծային կարգը... Հարաբերությունները կոչվում են կապված X բազմության վրա, եթե x և y որևէ տարրերի համար պայմանը բավարարված է, այն փաստից, որ x ≠ y հետևում է, որ x R y կամ y R x: Եթե ​​բազմության վրա տրված է գծային կարգի հարաբերություն, ապա այն գծային կարգով պատվիրում է տվյալ բազմությունը։

5. Իրական թվերի բազմությունը. Դրա հատկությունները... Հատվածների, մակերեսների և այլնի երկարությունները չափելու անհրաժեշտությունը հանգեցրեց ռացիոնալ թվերի բազմության ընդլայնմանը։ Ցանկացած չափում հիմնված է նույն սկզբունքի վրա. չափված օբյեկտը համեմատվում է ստանդարտի (օբյեկտի կամ երևույթի) հետ, որի արժեքն ունի 1-ի թվային արժեք, բայց ոչ միշտ է, որ չափվող օբյեկտում միավոր հատված է ներդրվում: Հետևաբար, չափելիս արվում է 2 ենթադրություն, որոնք մաթեմատիկայի մեջ սահմանվում էին որպես աքսիոմներ. 2) Ցանկացած մեծ օբյեկտ կարող է չափվել ընտրված ստանդարտով: Հատվածների համար այս աքսիոմները ձևակերպվել են Արքիմեդի կողմից. Անկախ նրանից, թե որքան փոքր է AB հատվածը և որքան էլ մեծ է հատվածը SD, կա N բնական թիվ այնպես, որ N * AB> CD, եթե չափված հատվածը CD պարունակում է հավասար թվով հատվածները AB, ապա CD հատվածի երկարությունը արտահայտվում է բնական թվով։ Եթե ​​չափված CD հատվածում AB հատվածը դրված է անհավասար թվով անգամ, ապա AB-ն բաժանվում է 10 նույնական հատվածների, որոնք կոչվում են ստանդարտների տասներորդ: Անհրաժեշտության դեպքում տասներորդ մասը կարելի է բաժանել 10 հավասար մասերի և այլն։ Եթե ​​CD հատվածը պարունակում է հավասար թվով 10, 100 և այլն: AB հատվածների բաժնետոմսերը, ապա CD հատվածի երկարությունը արտահայտվում է ռացիոնալ թվով: Այնուամենայնիվ, հատվածի երկարությունը միշտ չէ, որ կարող է արտահայտվել որպես բնական կամ ռացիոնալ թիվ: Կան անհամեմատելի հատվածներ, այսինքն. հատվածներ, որոնց երկարությունը ռացիոնալ թվով չի արտահայտվում։ (թեորեմների համար տե՛ս հարցը 32)

Այն թվերը, որոնք կարող են ներկայացվել որպես անվերջ տասնորդական ոչ պարբերական կոտորակներ, կոչվում են իռացիոնալ։ Ռացիոնալ թվերի բազմության և իռացիոնալ թվերի բազմության միավորումը իրական թվերի բազմությունն է ():

Իրական թվերի բազմության հատկությունները... մեկը): Թվային առանցքի կետերի բազմությունը հավասար է իրական թվերի բազմությանը։

0 М 1 Վերցրեք ցանկացած М կետ 0-ից 1 հատվածի վրա,

D գծեք կիսաշրջան, որի կենտրոնում

Այս գծի կեսը և շառավիղը

ԿՈՍ-ը հավասար է դրա կեսին։ M-ից կիսաշրջանով հատվող հատվածին ուղղահայաց գծե՛ք: Մենք ստանում ենք D: Այս կետը եզակի է, քանի որ կիսաշրջանն ու ուղիղը հատվում են միայն մեկ կետում: Այս հատվածի կեսից մինչև D-ը մենք ուղիղ գիծ ենք գծում դեպի թվային առանցքի հատումը: Մենք ստանում ենք K, որը եզակիորեն որոշված ​​է, քանի որ ուղիղները հատվում են միայն մեկ կետում: Ընտրելով մեկ այլ կամայական կետ տվյալ հատվածի վրա և կրկնելով ամբողջ գործընթացը՝ մենք ստանում ենք, որ 0-ից 1 հատվածի ցանկացած կետ համապատասխանում է թվային ուղիղի մեկ կետին: Հակառակ կարգով վիճելով՝ կարելի է ցույց տալ, որ թվային ուղղի ցանկացած կետ նույնպես համապատասխանում է 0-ից 1-ի մեկ կետի: Եթե կամայական E կետը պատկանում է թվային ուղիղին, ապա M և E կետերի միջով կարող է միայն մեկ ուղիղ. գծված լինի, որը հատում է կիսաշրջանը։ Կիսաշրջանից դուք կարող եք իջեցնել ուղղահայացը տվյալ հատվածին: Այսպիսով, 0-ից 1 հատվածի կետերի և թվային գծի կետերի միջև հաստատվում է փոխադարձ նույնական քարտեզագրում, այսինքն. նրանք նույնքան հզոր են:

2) իրական թվերի բազմությունը հաշվելի չէ, այսինքն. այն հավասար չէ բնական թվերի բազմությանը։

3). Իրական թվերի բազմությունը շարունակական բազմություն է։ Իրական թվերի բազմության շարունակականությունն այն է, որ ցանկացած երկու իրական թվերի միջև կա միայն իրական թվերի անսահման բազմություն.

6. Հավաքածուի բաժանում դասերի: Դասակարգման օրինակներ. Համարժեքության կապը, նրա հատկությունները. Համարժեքության կապի փոխկապակցվածությունը բազմության դասերի բաժանման հետ։ Դիտարկենք մի օրինակ։ Թող տրվի M բազմություն (ուռուցիկ բազմանկյունների բազմություն), մենք կազմում ենք այս բազմության բոլոր ենթաբազմությունները՝ A 1 - եռանկյունների բազմություն; A2 - քառանկյունների հավաքածու; A3 - հնգանկյունների հավաքածու; Ak-ը k-gon-ների բազմություն է: M բազմությունը համարվում է բաժանված դասերի, եթե բավարարված են հետևյալ պայմանները.

1. յուրաքանչյուր Ա ենթաբազմություն դատարկ չէ
2. Ցանկացած երկու ենթաբազմությունների խաչմերուկը դատարկ բազմությունն է
3. բոլոր ենթաբազմությունների միավորումը տրված բազմություն է Մ

Բազմաթիվը դասերի բաժանելը կոչվում է դասակարգում.

Վերաբերմունք X բազմության վրա կոչվում է համարժեք եթե այն ռեֆլեկտիվ է, սիմետրիկ և անցողիկ։ Հարաբերությունները կոչվում են արտացոլողեթե X բազմությունից որևէ տարր իր հետ կապված է a ∈ X, իսկ R a (R-ը հարաբերության մեջ է): Հարաբերությունները կոչվում են սիմետրիկեթե X բազմության ցանկացած երկու տարրի համար (a և b) այն փաստից, որ a-ն առնչվում է c in-ին, հետևում է, որ b-ն առնչվում է a-ին (a, b ∈ X և R-ը → R a-ում) . Հարաբերությունները կոչվում են անցողիկեթե որևէ a, b, c տարրերի համար, այն փաստից, որ a R-ն և R-ում c → որ a R c, a, b, c ∈ X: Համարժեքության հարաբերության գրաֆիկի վրա կան օղակներ, փոխադարձ հակադարձ սլաքներ և եռանկյունաձև նետերը. Համարժեքության հարաբերությունը և միայն այն կապված է բազմության դասերի բաժանման հետ։ Այս հայտարարությունը կարելի է ձևակերպել այսպես թեորեմներԵթե ​​X բազմության վրա տրված է համարժեքության առնչություն, ապա այս հարաբերությունը բաժանում է X բազմությունը դասերի, և հակառակը, եթե X բազմությունը բաժանվում է դասերի, ապա համարժեքության կապը կատարվում է տվյալ բազմության վրա։ Օրինակ. Թող վերաբերմունքը տրվի՝ ապրել նույն տանը։ Եկեք ցույց տանք, որ տան շատ վարձակալներ բաժանվելու են դասերի: Իսկ ամեն դասը առանձին բնակարան է։ Այս բաժանման համար կբավարարվեն բազմությունը դասերի բաժանելու բոլոր անհրաժեշտ պայմանները. ա) յուրաքանչյուր դաս դատարկ չէ, քանի որ. յուրաքանչյուր բնակարանում կա առնվազն 1 հոգի, բայց գրանցված է, բ) դասերը չեն համընկնում (1 անձ գրանցված չէ երկու տարբեր բնակարաններում), գ) բոլոր դասերի միավորումը, այսինքն. յուրաքանչյուր բնակարանի վարձակալները և կազմում են տան բազմաթիվ վարձակալները:

18 ... Բազմաթիվ-տեսական մոտեցում ոչ բացասական ամբողջ թվերի տեսության կառուցմանը: Հավասարության հարաբերություններ, ավելին (պակաս): Երկու A և B բազմությունները կոչվում են համարժեք կամ հավասար ուժով, եթե հնարավոր է դրանց միջև մեկ առ մեկ համապատասխանություն հաստատել, այսինքն, եթե A բազմության յուրաքանչյուր տարր կապված է B բազմության մեկ տարրի հետ և հակառակը: . Կարդինալությունը կամ հիմնական թիվը հատկություն է, որը բնորոշ է ցանկացած B բազմությանը, որը հավասար է A բազմությանը և բնորոշ չէ որևէ այլ բազմության, որը հավասար չէ A բազմությանը: A ~ B n (A) = a-ն կարդինալություն է: . Համարժեքության հարաբերակցությունը համարժեքության հարաբերակցություն է, այսինքն. դրա համար կատարվում են ռեֆլեքսիվության, համաչափության և անցողիկության հատկությունները։ Հավասարության հարաբերությունը բոլոր բազմությունների բազմությունը բաժանում է համարժեքության դասերի: Բնական թվի և զրոյի հասկացությունը սահմանելու համար դիտարկենք բոլոր վերջավոր բազմությունների բաժանումը:

Թող M լինի բոլոր վերջավոր բազմությունների բազմությունը: M = K 0 Ka Kv, որտեղ Ko-ն դատարկ բազմությունների դասն է, Ka-ն մի շարք է, որը պարունակում է նույնքան հզոր բազմություններ a 1, a 2, a 3 և այլն, Kb-ն բազմություն է: Նույնքան հզոր հավաքածուներ պարունակող 1-ում, 2-ում, 3-ում և այլն: M բազմությունը կարող է պարունակել նաև K-ի տարբեր բնույթի այլ ենթաբազմություններ, որոնք բաղկացած են նույնքան հզոր բազմություններից։ K համարժեքության յուրաքանչյուր դասի ընդհանուր առանձնահատկությունն այն է, որ դրանք բաղկացած են նույն թվով տարրերից, այլ ընդհանուր հատկություններ չկան: Բազմությունների տեսական տեսանկյունից ոչ բացասական ամբողջ թիվը վերջավոր հավասարազոր բազմությունների դասի ընդհանուր հատկությունն է։ Բնական թիվը ոչ դատարկ վերջավոր հավասարապես հզոր բազմությունների դասի ընդհանուր հատկությունն է։ Յուրաքանչյուր դասի նշանակվում է կարդինալ համար (կարդինալություն): Դասի դատարկ բազմությանը վերագրվում է կոորդինացիոն համարը 0։ 1 տարր ունեցող բազմություններից բաղկացած դասին վերագրվում է 1 թիվը։ 2 տարր ունեցող բազմություններից բաղկացած դասին վերագրվում է 2 թիվը. (n (K 0) = 0, n (K 1) = 1, n (K 2) = 2, n (Ka) = a):

Հավասարության հարաբերություն... Ոչ բացասական a և b ամբողջ թվերը կոչվում են հավասար, եթե A և B բազմությունները, որոնց թվերը նրանք արտահայտում են, հավասար են (A; n (A) = a, n (B) = b, A ~ B n ( A) = n (B) a = b).

ԹեորեմՈչ բացասական ամբողջ թվերի բազմության հավասարության հարաբերությունը համարժեքության հարաբերություն է։ Ապացույց... Փաստենք, որ հավասարության հարաբերությունն ունի համաչափության, անցողիկության և ռեֆլեքսիվության հատկություններ։

Որովհետեւ ռեֆլեքսիվության, համաչափության, անցողիկության հատկությունները կատարվում են, ապա հավասարության կապը համարժեքության հարաբերություն է։

Հարաբերակցությունը պակաս... Ոչ բացասական ամբողջ թիվ ա<в, если множество А равномощно собственному подмножеству В 1 множества В. а<в; n(А)=а; n(В)=в; В 1 В n(В 1)

Թեորեմ. ոչ բացասական ամբողջ թվերի բազմության մեջ պակաս հարաբերակցությունը խիստ կարգավորված հարաբերություն է: Ապացույց. Փաստենք, որ կապն ունի ավելի քիչ հակասիմետրիկ և անցողիկ հատկություններ:

C 2 C 1 C 2 ~ B 1 C 2 ~ A n (A) = n (C 2) n (C 2)

A B C 1 C

B 1 C 2

19 . Ոչ բացասական ամբողջ թվերի քանակական տեսության մեջ գումարում և հանում. Նրանց հատկությունները. Գումարըերկու ոչ բացասական a և b ամբողջ թիվը կոչվում է ոչ բացասական ամբողջ c, որը A և B երկու անհամապատասխան բազմությունների միավորման հիմնականությունն է, որոնց կարդինալությունները համապատասխանաբար հավասար են a և b-ի: a + b = c, n (C) = n (AUB), n (AUB) = n (A) + n (B):

Ծալովի հատկություններ... 1. Ոչ բացասական ամբողջ թվերի բազմության մեջ գումարումը միշտ գոյություն ունի և եզակիորեն որոշվում է: Ապացուցենք, որ գումարը միշտ կա։ Դիտարկենք A-ն և B-ն այնպես, որ դրանց հատումը դատարկ բազմություն է, և A-ի տարրերի թիվը՝ a, իսկ B-ի կարդինալությունը՝ b: մենք գտնում ենք A-ի և B-ի միությունը: Քանի որ երկու տարանջատված բազմությունների միությունը միշտ կա, ինչը նշանակում է, որ գումարը նույնպես գոյություն ունի, և գումարի սահմանումից հետևում է, որ գումարումը միշտ գոյություն ունի:

Փաստենք, որ գումարը եզակիորեն որոշված ​​է։ Կան C 1 և C 2 - ոչ բացասական ամբողջ թվեր: C 1 = a + b և C 2 = a + b: a և b թվերի գումարը կախված չէ նրանից, թե որ A և B բազմություններն ենք ընտրել համարժեք բազմությունների դասից, և հետևաբար համարժեք բազմությունների դասից վերցված A և B միավորումը կախված չէ բազմությունների ընտրությունից։ A և B, քանի որ յուրաքանչյուր դասի կարդինալությունը նույնն է, ապա C 1 = C 2:

2. Հավելման հրմշտոց. Ցանկացած ոչ բացասական a և b ամբողջ թվերի համար գործում է a + b = b + a հատկությունը: Բազմությունների տեսությունից մենք գիտենք, որ AUB = BUA-ի համար: Եթե ​​բազմությունները հավասար են, ապա դրանց թվային արժեքները հավասար են: n (AUB) = n (BUA): Բազմությունների տեսությունից մենք գիտենք, որ միության կարդինալությունը հավասար է կարդինալությունների գումարին: N (A) + n (B) = n (B) + n (A):

3. Ասոցիատիվության սեփականություն. a, b, c ցանկացած թվերի համար գործում է հետևյալ հատկությունը՝ a + (b + c) = (a + b) + c: Բազմությունների տեսությունից հայտնի է, որ բազմությունների միավորման համար կատարվում է ասոցիատիվ հատկություն՝ AU (BUC) = (AUB) UC, եթե բազմությունները հավասար են, ապա դրանց թվային արժեքները հավասար են՝ n (AU (BUC)) = n ((AUB) UC): Բազմությունների տեսությունից հայտնի է, որ միության կարդինալությունը հավասար է այս բազմությունների կարդինալությունների գումարին, n (A) + n (BUC) = n (AUB) + n (C) n (A) + (n): (B) + n (C)) = (n (A) + n (B)) + n (C) a + (b + c) = (a + b) + c.

Տարբերությունոչ բացասական a և b ամբողջ թվերը ոչ բացասական ամբողջ c թիվ է, որը B բազմության լրացման կարդինալությունն է A բազմությանը, այնպես, որ B-ն պատկանում է A-ին, n (A) = a, n (B) = բ.

Տարբերության հատկություններ... 1. Որպեսզի գոյություն ունենա ոչ բացասական ամբողջ թվերի տարբերությունը, անհրաժեշտ և բավարար է, որ a-ն մեծ կամ հավասար լինի b-ին:

Եկեք ապացուցենք 1) բավարար պայման տարբերության առկայության համար. Տրված է՝ a - b = c, ապացուցել՝ a c. Տարբերության սահմանումից հետևում է, որ կա B բազմության լրացում A բազմությանը, և այս լրացումն ունի կարդինալություն, որը կարելի է գտնել բազմությունների տեսությունից հայտնի հավասարությունից։

n () = n (A) -n (B): Քանի որ B-ն A-ի ենթաբազմությունն է, հետևաբար, B-ի տարրերի թիվը փոքր է A-ի տարրերի քանակից: n (B) v; B-ն ներառված է A-ում; n (B)

2). Անհրաժեշտ պայման. Տրված է Ա.Վ. ապացուցել տարբերության առկայությունը (ab). Եթե ​​a> b, ապա «պակաս» հարաբերակցության սահմանմամբ կա A 1 այնպիսի բազմություն, որ A 1-ը ներառված է A-ում և A 1 ~ B-ում: Եկեք կազմենք A-ի և A 1-ի տարբերությունը: Այս տարբերությունը միշտ կա (A - A 1 = C), և, հետևաբար, կա C, որն այս տարբերությունն է: Այս պայմաններից հետևում է, որ C-ն A 1-ի լրացումն է A-ին: C = 1A C-ի հզորությունը A 1-ի A լրացման հզորությունն է: n (C) = n (1A) = n (A) -n (A 1), քանի որ A 1 ~ B, ապա n (A 1) = n (B), հետևաբար n (C) = n (A) -n (B), հետևաբար c = ab.

2. Ոչ բացասական ամբողջ թվերի տարբերությունը եզակի է, քանի որ տարբերությունը մի բազմության ենթաբազմությունների լրացման կարդինալությունն է, և լրացումը որոշվում է եզակի, ապա ոչ բացասական ամբողջ թվերի տարբերությունը որոշվում է եզակի:

3. Հանման համար կոմուտատիվության և ասոցիատիվության հատկությունները բավարարված չեն:

4. Թվից հանելով գումարը. a- (b + c) = (a-b) -c. Բազմությունների տեսությունից հայտնի է, որ A \ (BUC) = (A \ B) \ C և B Ì A; C Ì A; ВUСÌА.

n (A \ (BUC)) = n ((A \ B) \ C)

n (A) -n (BUC) = n (A \ B) -n (C)

n (A) - (n (B) + n (C)) = (n (A) -n (B)) - n (C)

a- (b + c) = (a-b) -c.

5. (a-c) -c = (a-c) -c տարբերությունից հանելով թիվը: Ապացույցը հիմնված է բազմությունների տարբերության հատկության վրա (A \ B) \ C = (A \ C) \ B:

6. Թվի հանում (a + b) -c = (a-c) + b. Ապացույցը հիմնված է բազմությունների հատկության վրա (AUB) \ C = (A \ C) UB:

Անջատել adBlock-ը:
շատ անհրաժեշտ